2019.01.09 - [컴퓨터 사이언스 부트캠프 with 파이썬] - Study02

본 포스팅은 컴퓨터 사이언스 부트캠프 with 파이썬 이라는 책을 참고하여 개인 공부를 하면서 정리하고 있습니다. 문제 될 시 삭제하겠습니다.

정수와 실수

보수

컴퓨터에서는 부호를 표현하기 위해 맨 앞 비트를 부호 비트로 사용한다. 0은 양수, 1은 음수이다.

그리고 여기서 보수(Complement)의 개념이 등장한다. 보수의 뜻은 ‘보충해 주는 수’라는 의미이다. 9의 보수라고 하면 각 자리의 합이 9가 되는 수이다.

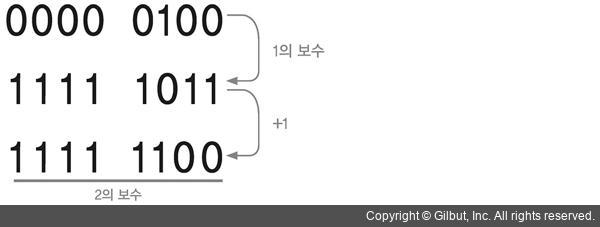
하지만 우리에게 중요한 것은 9의 보수가 아니다. 컴퓨터는 0, 1 밖에 사용하지 못하므로 2진수의 2의 보수(two’s complement)가 중요하다. 먼저 2의 보수를 구하기 위해서는 1의 보수를 먼저 구해야한다. 1의 보수는 각 자리수를 뒤집은 것과 같다. 2의 보수는 1의 보수에서 1만 더해주면 된다. 이렇게 구한 2의보수는 컴퓨터가 음수를 사용할 때 사용한다.

컴퓨터가 부호비트 자리의 0과 1로 양수와 음수를 표현하는데 왜 보수를 사용하는지 의문이 생길 수 있다. 이유는 다음과 같다. 예를 들어 1과 -1을 보수의 개념 없이 부호비트만으로 표현한다고 생각해보자(8bit 라고 가정해보자). 양수 1은 0000 0001로 표현된다. 음수 -1은 1000 0001이라고 표현될 것이다(물론 이렇게 절대 표현되지 않는다). 이 둘의 합을 구하면 1 + (-1) = 0이 나와야한다. 하지만 2진수로 표현된 두 값은 1000 0002가 나온다. 뭔가 이상하지 않은가? 이 2진수 값은 0이 아니다. 따라서 -연산을 할 수 없는 논리적 오류가 발생한다. 따라서 이를 방지하기 위해 컴퓨터는 보수의 개념을 도입하여 사용하는 것이다.

부동소수점

부동소수점은 소수점의 위치가 정해지지 않았다는 뜻이다. 아래의 그림을 통해 간단하게 이해하고 넘어가자.

단정도와 배정도

부동소수점에는 단정도 부동소수점과 배정도 부동소수점이 있다. 단정도는 실수를 32비트(4바이트)로 표현하며 부호 1비트, 지수부 8비트, 가수부 23비트로 구성된다.

배정도 부동소수점은 실수를 64비트(8바이트)로 표현하며 부호 1비트, 지수부 11비트, 가수부 52비트로 구성된다.

이 배정도 부동소수점은 단정도 부동소수점에 비해 실수를 표현하는 데 사용하는 비트 수가 두 배 많은 만큼 정밀도가 더 높다.

부동소수점의 정밀도와 메모리

1바이트 부동소수점은 아래와 같이 구성된다.

4바이트 부동소수점은 아래와 같이 구성된다.

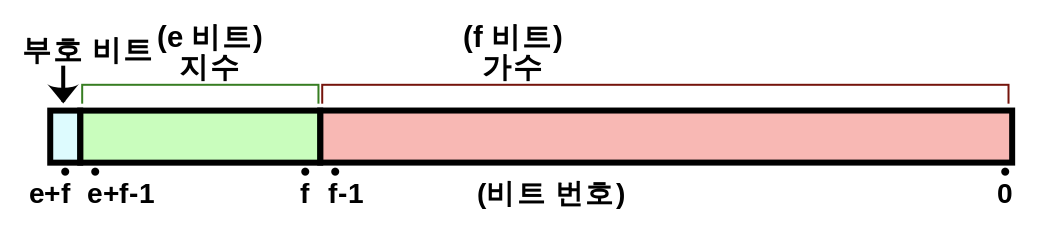
먼저 부동소수점에서 첫 번째 비트는 부호를 나타낸다. 0이면 양수, 1이면 음수이다. 가운데 4비트는 지수부로 exp값을 나타내고 맨 뒤 3비트는 가수부로 정규화 한 수에서 소수점 왼쪽의 가수를 나타낸다.

exp값은 지수와 bias값을 더해서 구한다. 여기서 bias 값은 2^(n-1) - 1 로 구한다. n은 지수부의 비트 수 이다. bias는 지수의 부호를 결정하는데 사용된다. 부동소수점의 지수부에는 부호 비트가 없으며 (1바이트 부동소수점에서는) 0~15의 양수만 나타낼 수 있다. 하지만 지수에는 음수도 존재한다. 음수를 사용하기 위해 bias를 7로 두고(4비트 부동소수점에서는 bias를 127로 둔다) 지수부(exp)에서 bias를 뺀 값을 실제 지수로 사용한다. 이를 토대로 7.75를 1바이트 부동소수점 방식으로 표현하면 다음과 같다.

1. 7.75를 먼저 2진법으로 변경한다. »> 111.11
2. 이를 정규화 시켜준다. »> 1.1111 * 2²
3. 정규화된 값을 가지고 부호, 지수부, 가수부를 정해준다.
4. 부호 -> 0, 지수부 -> 1001, 가수부 -> 1111
5. 여기서 가수부가 3비트만 할당되므로 뒷자리 1을 생략해준다. 가수부 -> 111
6. 부동소수점 0 1001 111
7. 이진수 0100 1111를 16진수로 변환하면 0x4f이다.

부동소수점을 계산할 때는 보수의 개념을 사용하지 않는다.

엡실론과 정밀도

엡실론(epsilon)

엡실론이란 1.0과 그 다음으로 표현 가능한 수 사이의 차이를 말한다. 이 엡실론은 실수들의 정밀도를 표현하는데 사용된다.

배정도 실수 9.25를 부동소수점 방식으로 표현하면 1.00101 * 2³ 이다. 위 식에서 지수 부분만 떼어 내 엡실론을 곱하면 이 실수와 다음 표현 가능한 수 사이의 차이를 구할 수 있다.

>>> import sys
>>> ep = sys.float_info.epsilon
>>> a = 9.25
>>> diff = (2**3)*ep
>>> diff
1.7763568394002505e-15
>>> b = a + diff
>>> b
9.250000000000002

epsilon은 1.0과 그 다음 수의 표현 가능한 수의 차이다. 따라서 위 식은 지수 부분이 1.0 * 2⁰ 이 아니라 (1.0) * 2³ 이므로 1.0 * 2³ * epsilon을 해줘야 2³ 만큼 소수점이 움직인 epsilon을 구할 수 있다.

위 식에서 diff는 지수 부분인 2³ 에 엡실론을 곱한 값으로 9.25와 그 다음 표현 가능한 수 사이의 차이이다. 만약에 9.25에 diff보다 작은 값을 더하면 부동소수점 방식에서는 이 값을 다르게 표현 할 방법이 없다. 예를 들어 9.25에 diff/2 더한 값과 9.25을 비교해도 두 값은 같다고 컴퓨터는 인식한다. 왜냐하면 표현 가능한 수의 차이 보다 작은 값을 더했기 때문에 컴퓨터가 인식하지 못하기 때문이다.